１万票差でも当選確実が出せるワケ

こんばんは。最近めっぽう暑くて困ってしまいますね。

暑いといえば、こないだの大阪都構想選挙は予想以上にアツい戦いとなりましたね。関係者でもないのに、ハラハラしながら見てしまいました。ところで、開票速報を見ていて、いきなり『多数確実』と表示されてびっくりしたのは、わたしだけではないかと思います。

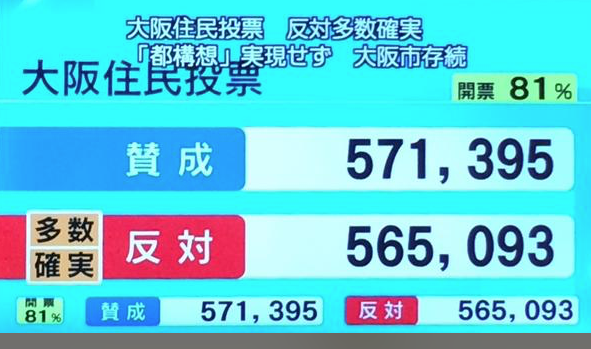
こんなに接戦な上に、どうして残り19%も未開票なのに、多数確実なんだろう？ヽ(`Д´)ﾉ　と思われた方も多いのでは無いでしょうか？？

そこで、今回はいわゆる『当選確実』がどのように出るのかについて、考えてみました。

『当選確実』の統計学

開票速報を行い、投票数の50%を取れば、他の票全てが反対側に回っても結果が覆ることは無いため、『当選確定』と言えます。一方、『当選確実』はこれまでのデータから、他の票数の動きを予想しても『ほぼ間違い無いでしょう』といえる状態です。

統計の世界では、『少ないサンプルから全体を予想する』といったことを良く行います。例えば、『テレビの視聴率』は、全世帯のデータを集めているわけではないですし、『LED電球の平均寿命』も一部のサンプルでテストして計測します。(全員に聞いてたらコストが掛かり過ぎますし、全部テストしたら出荷できる製品がなくなります。）

全数調査を行わない以上『絶対にこの値が正解』ということはありえません。そこで、ある一定許容誤差の範囲を設けて、その範囲内に収まる結果を得るために必要なサンプル数を計算し、抜き取り検査を行うわけですね。

さて、許容誤差と予測される値の関係ですが、許容誤差が大きければ大きいほど、予測される値のレンジは小さくなります。そして、その逆もしかりです。

例えば、明日の売り上げ予想を指示されたとします。その時、『やんわり90％くらいの確率で当たる場合でいいから』と言われれば、『ベストシナリオで110万円、ワーストシナリオで90万円くらいですかね？』となりますが、『レアなケースも考慮して、99%あり得る範囲を予想してね』と言われれば、『うーん・・・、最善でも120万円、最悪なら80万円でしょうか？』という回答になると思います。

 こういった分野を、一生懸命研究してきた分野が『統計学』です。では、統計的に今回の81%で『多数確実』と発表されたことが、どの程度『あり得る』確率なのか考えてみたいと思います。

統計学が最強の学問である

１万票差の許容誤差

では、今回の選挙で『多数確実』が出たタイミングについて考えてみます。まず、NHK発表段階の数値では、『賛成』が『反対』を上回っています。これは、投票所毎の開票速報のタイミングの違いによるものでしょう。

ここでは、開票速度のスピードにバラつきがないものと想定し、それぞれのタイミングにて、最終的な得票率と同じ値が得られていたものとします。

確認になりますが、最終的な結果としては、反対は50.384%でした。ということは、反対が、『相当高い割合で、0.384%以上反対の票数が減ることはありえない』ということが説明できれば、『多数確実』ということが出来そうですね。

サンプル数が少なければ、『たまたま抜き取ったデータに偏りがあったのかも』と言えてしまうので、『これだけ確認して、間違いがなければ、多少誤差があったとしても確実でしょう』という値を求めます。

ここでは、以下の数式を元に、誤差の範囲を求めます。（本当は、色々と前提条件もあるのですが、この数式に全て当てはめられるものとして計算します）いわゆる、二項分布の推定、ってやつですね。

ｔ＊√（標本比率＊（１−標本比率）÷標本数）
tの値　(付表： t分布表 Student's t distribution — 中川雅央（滋賀大学）

細かい意味については、それを説明することが目的では有りませんので、割愛いたします。

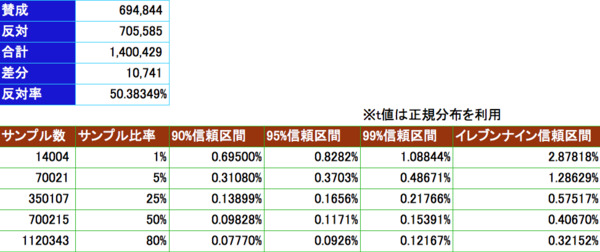
上の表は、サンプル数と、◯◯%信用出来る値が欲しい場合の予想誤差の範囲について、まとめたものです。(なお、99.999999999%のことを9が11個でイレブンナインと呼びます。)

まず、サンプルが全体の1%だと、本当に反対が50.383%かと言われると、自信が持てないですよね。10%くらいは外してもいいから！と言われても、±0.695%くらいの誤差はあるかと・・・と言うしか有りません。

では、どんどんサンプルを増やして、5%だとどうでしょう。10%くらい外してもいいのであれば、±0.3108%となり、常に反対が50%を超えます。ただこのレベルだと、99%まで信頼できる値か？と言われると、最大±0.48671%までズレこむことが考えられ、『確実』というと二の足を踏む水準です。

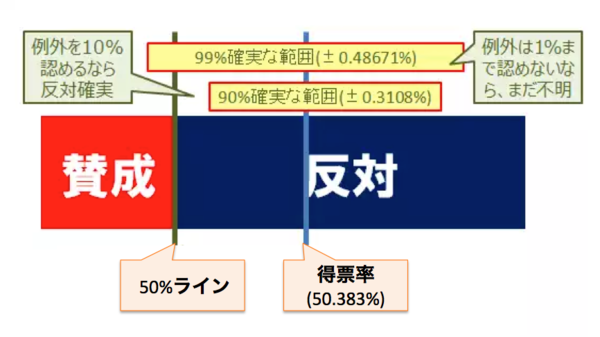
じゃあ、多数確実のでた80%だとどうでしょう？こうなると、イレブンナインな水準でも、『0.000000001%の例外が出ない限り、多数確実』ということが出来ますので、安心して発表出来ますね。流石に、80%も開票してしまえば、相当のことが無い限り覆らない結果が得られそうですね。

（なお、実際には開票所ごとにこの分析を行い、その許容誤差が積み重なっるはずですので、もう少し誤差は大きくなるかもですね。）

『当選確実』の重み

さて、実際の当選確実については、

• 出口調査の結果
• 事前の大規模な組織の動向分析
• 開票所に積まれた票の山のサイズ

なども用いて、発表を行うそうです。ただ実際には、当選確実の発表には、ミスもあるそうです。

gohoo.org

こういった誤報があると、『なーんだ、がっかり』といったレベルでは済まない影響が発生してしまいます。一番確実なのは、『統計的に有意な水準』まで、実際の開票データを積み上げてから行うことですが、報道各社は1秒でも早く『当選確実』と出したいため、フライングもあるようです。

実際に、中で何をやっていたかは、『中の人ぞのみ知る』ですが、選挙の結果について、統計的に考えてみるのも中々面白いのではないでしょうか？

ではでは、皆様のご参考になれば幸いです。