こんにちは、らくからちゃです。
原価コンサルタント見習として、コスト・マネジメントのお手伝いをさせて頂いております。売上が増えても、製品を作るのに高い材料が必要だったり、工程が複雑で人件費が掛かるようだと利益には繋がりませんよね?そこで製品ごとに製造コストを計算して『いくらなら利益が出るのか?』『いま一番儲かっている製品はどれか?』といったことを分かりやすくお伝えするシステムの導入を支援させて頂いております。
お客様に『このコストは、この実績に連動して増減するから、これを基準に按分して...』なんてヒアリングをしながら設定作業を進めていくのですが、本当にその考え方で良いのかなあなんて思うことはよくあります。そんなモヤモヤした気持ちを抱えながら本屋さんに行った所、なかなか面白い本を発見いたしました。
データが連動するからといって因果関係があるとは言えないよね!
分かっている人からすれば、何を今更と思うのかもしれませんが、以下の調査結果を元に因果と相関の違いについて順を追って丁寧に解説されています。
- メタボ検診を受けていれば長生きできるのか
- 男性医師は女性医師より優れているのか
- 認可保育所を増やせば母親は就業するのか
- テレビを見せると子どもの学力は下がるのか
- 勉強ができる友人と付き合うと学力は上がるのか
- 偏差値の高い大学に行けば収入は上がるのか
それぞれの具体的な内容については本書の解説に譲るとして、テーマである相関と因果の違いについて簡単にまとめてみます。
ビールが売れればアイスクリームが売れる?
我々はなんのために、手間暇をかけて数字を整理するのでしょうか?それは、異なる複数の事象の間に関連性を見つけて将来を予測し、より少ない努力で大きな成果を得るためではないでしょうか。特にグラフを用いて可視化すれば、手軽に分析ができ多くの人に分かりやすく関連性を伝えられます。
例えば、ある年の商品の売上データを並べてみると、どうやらビールとアイスクリームの売上の間に、何らかの関連性があることが分かりました。
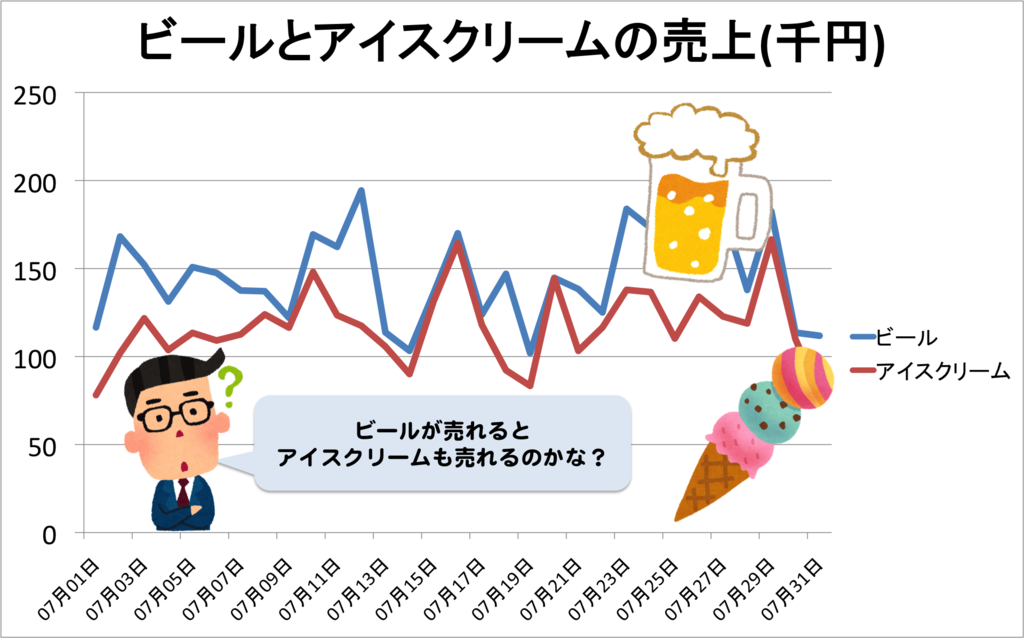
保管に電気代も掛かるので在庫は必要最小限に抑えたいと思っています。しかし欠品すると機会損失に繋がります。そこで、このグラフを見た発注担当者は『なるほど。ビールが売れる時にアイスクリームも売れるんだ。近いうちに宴会で大量にビールの注文が来ていたな。アイスクリームの発注も増やしておこう!』と言ったらどう思います?
ビール飲むんだったらアイスクリームも食べたいなー!!ってなりますかね。多分違いますよね。どちらも暑い日に売れるのであって、ビールが売れるだけだとアイスクリームの売上には関係しない。宴会でビールの注文が増えたからアイスクリームの発注増やしても売れない可能性が高いのではないでしょうか。
こういった原因と結果の双方に影響をあたえる要素を『交絡因子』と呼びます。ある数値と別の数値が連動して変化していたとしても、その他の要因も含めて考えないと、間違った判断をすることに繋がりかねません。
じゃあ、ビールと焼鳥なら?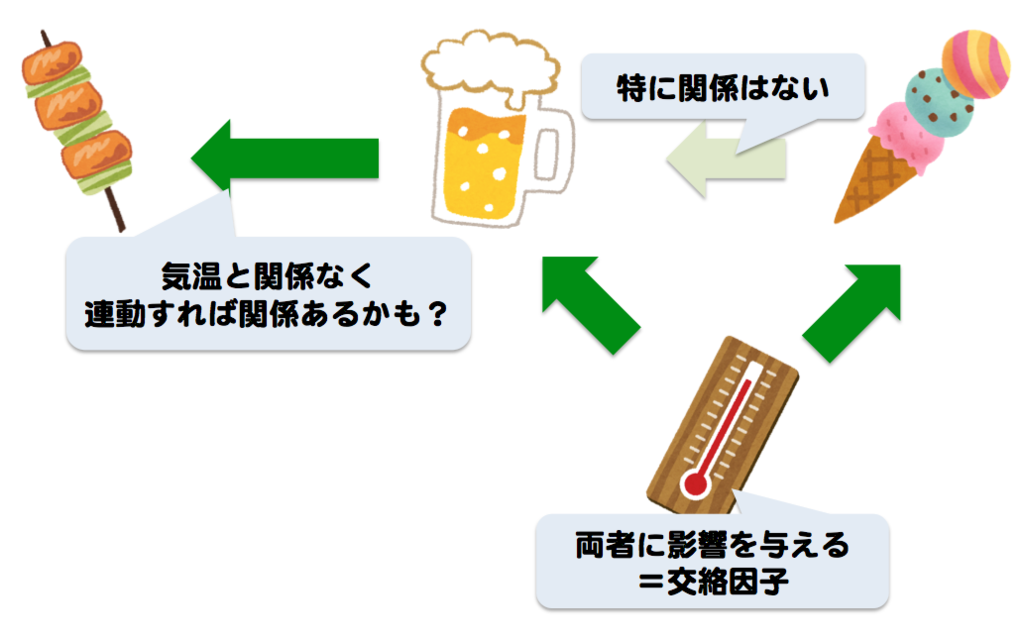
気温や客数、他の商品の売上に関係なく『ビールが売れれば焼き鳥も合わせて売れる』という結果が出れば、ビールの需要に合わせて焼き鳥を発注しておけば上手く儲かるかもしれませんね(宴会のお客さんにまで売れるはわかりませんが・・・)
2つの要素の間に原因と結果の関係になるものを『因果関係』があると言い、ただ単純に数値が連動しているだけの関係は『相関関係』と言います。この2つを見分け『本当にそのデータの読み解き方は正しいんだろうか?』ということについて考える方法論を『因果推論』と呼びます。本書でも色々な事例からその手法について取り上げられていますが、日常生活でも簡単に使える3つのチェックポイントが挙げられていましたのでご紹介します。
因果関係を確認する3つのチェックポイント
1.『まったくの偶然』ではないか
連動して動く2本の折れ線グラフは何か神秘的なように見えてしまい、ずーっと眺めていると『自分の知らない何かがあるのかもしれない』と思うこともあります。本書の中でも『気温と海賊の数』なんていう意味ありげで何も関係のないグラフが紹介されています。

(出典:「原因と結果」の経済学)
そんなときは一度冷静に『そもそも全くないものでも相関することはあるんだ』と落ち着いて考えることが大事です。
2.第三の変数は無いか
これは先程のビールとアイスクリームの関係における気温のようなケースの例ですね。確かに、2つの要素の間に関係は見られるものの、実はその背後に何か別の要素が無いのか?そこも考えてみる必要があります。
3.『逆の因果関係』は存在していないか
以前マネ会さんにこんな記事を投稿しました。
統計データを眺めていたら、年収の高い人ほど良く勉強をしてて面白いなーと思って書いた内容です。ただここでのポイントは
- 勉強している→年収があがる
- 年収が高い→勉強する余裕がある
のどちらなのか?についてはこのデータからだけでは判断することが出来ません。そこは騙されない(騙すつもりは無いのですが・・・)ようにする必要があります。
ちゃんとした分析にはコストが掛かる
さてこれらの前提のもと『本当に因果関係があるのか?』を確認しようとすると、かなりのコストがかかります。例えば『なんとこの商品を毎日食べるだけで、Aさんのお腹が1ヶ月でぺったんこに!』というCMを見たとします(よくありますよね)。そうするとあなたはこんな風に思うんじゃないでしょうか?
- 他の食事制限とかしてないの?
- Aさん以外はどうなのよ?
- 上手くいかなかったケースは無いの?
そういったことをちゃんと教えてくれないと、自分にも効果があるのか信じられませんよね。でもこれ、ちゃんと調べようと思うと
- 似たような条件の集団を2つ作る
- 片方には商品を食べて貰い、片方には食べさせない
といった分析を行わなきゃダメですよね。
こういった分析をランダム化比較試験といいます。さらに複数の試験結果のデータを集めてメタアナリシスという分析を行えば、ばっちり因果関係があることを証明できます。医学などの世界では、今までもこうした調査が行われてきましたが、経済学の世界ではこうしたことは余り行われず、統計調査のデータなどを元にした回帰分析程度が行われてきました。エビデンスのレベルにはある程度階層があります。
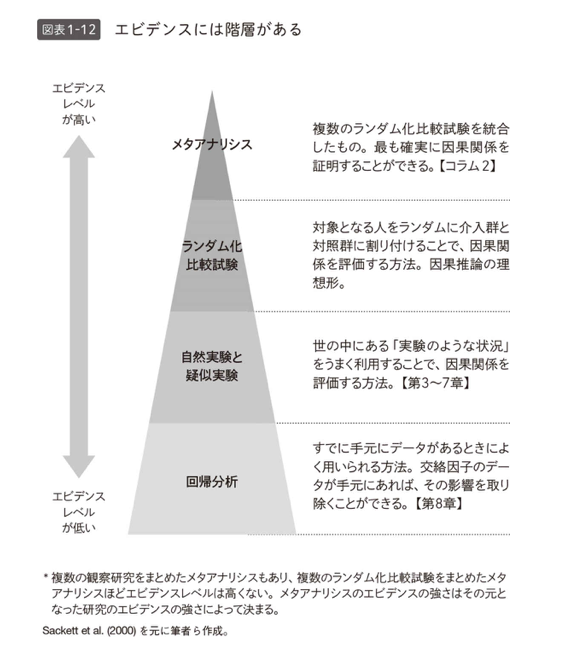
(出典:「原因と結果」の経済学)
ちゃんとした調査を行うには、調査内容の設計が重要です。研究室のプレパラートの上であれば、ある程度似たような試験を繰り返すことも出来ます。しかし生身の人間の属性の偏りをなくすためには、かなり大規模な社会実験になる場合もあります。
社会実験のコスト
オランダでこんな実験が行われたことがあります。
ただし、対象者は社会福祉受給者のみに限られるという。対象者の300人はいくつかのグループに分けて比較される。一つのグループには基本所得の約900ユーロ(約12万2500円。所帯がある人には約1200ユーロ=約18万円)を無条件で支給し、その他のグループは、さまざまな規則や条件のもとに支給する。
ベーシックインカムの支給条件による効果を分析するため、ランダム化比較試験を行ったわけですね。本来なら住民に平等であるべき行政が、ランダムに試験対象を差別するわけですから、下手をすると住民間の摩擦も生まれかねないので、慎重に行なう必要があります。
本書でも取り上げられていますが、過去にランド医療保険実験と呼ばれる調査が行われたことがあります。医療機関で支払う費用を
- 自己負担ゼロプラン
- 自己負担25%プラン
- 自己負担50%プラン
- 自己負担95%プラン
- HMOプラン(自己負担はゼロだが受診できる医療機関は制限される)
の5つにランダムに被験者を割り当て、医療機関の診療回数や健康への影響について分析した調査です。幸い各プランの間で、健康への影響は、あまり差が無かったようですが、低所得者の健康状態の悪い人たちでは自己負担率が低いほど健康への悪影響があったようです。(参考:医療保険の自己負担割合のインパクトを評価したランダム化比較試験「ランド医療保険実験」 – 医療政策学×医療経済学)
いくら世の中のためでも、自分や家族がその立場だったらと思うとゾッとしますね。
こうした調査は、金銭的・社会的なコストが大きくなりすぎる場合もあります。しかし得られる知見は大きな効果を生み出すことが出来る場合もあります。今後より多様化する社会のニーズに、限りある財源で対応するのであれば、こういった手法は経済学もより取り入れる必要はあるでしょう。
統計データの読み方と考え方
本書には、複雑なデータから真実を導き出すための手法について触りの部分がすごく分かりやすくまとめられています。
じゃあ、きちんと分析されたデータでなければ価値が無いのか?みんなで分析手法を学ばないといけないのか?というと、そういうわけじゃありません。なにより調査には大変コストが掛かりますので、まずはざっくりとあたりを付けるためにも手近なデータをもとに、みんなで考えていくことは大切です。
大切なことは、大事な意思決定をする前にちゃんとした調査を行い、本当に因果関係があるのかどうかをきちんと因果推論することじゃないでしょうか。

そこを考えるプロをきちんと育てることと。それが大事なんじゃないのかなあと思う今日このごろでございます。
ではでは、今日はこのへんで。
